Fin dalla comparsa del calcolo differenziale, inventato indipendentemente da Isaac Newton e Gottfried Leibniz verso la fine del diciassettesimo secolo*, le equazioni differenziali sono state utilizzate per gli scopi più diversi: dallo studio del moto dei sistemi planetari a quello della trasmissione di segnali fra le cellule nervose, dall’analisi delle dinamiche delle popolazioni biologiche alle stime delle fluttuazioni dei prezzi nei mercati economici. Le parole del matematico Vladimir Igorevič Arnol’d rendono l’idea dell’importanza di questo strumento più di qualunque elenco delle sue applicazioni:
Le equazioni differenziali formano la base della visione scientifica del mondo.
Non ci sarebbe dunque troppo da stupirsi se questo strumento così potente avesse già fatto capolino in un ambito dove la saggezza popolare vorrebbe invece che scienza (e ragione) abbiano ben poco da dire: la matematica dell’amore e la dinamica dei sentimenti.
Negli ultimi venti o trent’anni, in effetti, alcuni studiosi hanno iniziato a cercare di catturare in modelli matematici più o meno accurati tutti i sussulti, i sospiri, le esaltazioni e le disperazioni che caratterizzano lo stato dell’innamoramento. Vediamo un paio di esempi di modelli che tentano di descrivere – e soprattutto prevedere, come ogni buon modello scientifico dovrebbe fare! – l’andamento di una relazione sentimentale.
Il primo esempio risale al 1995, quando uno studioso di letteratura italiana fece appello alla matematica per tentare di risolvere il problema della datazione di molti componimenti del Canzoniere di Francesco Petrarca.
Ricordiamo che la raccolta di una delle opere più significative della storia della letteratura italiana comprende 366 tra sonetti, canzoni, sestine, ballate e madrigali, tutti scelti e ordinati dal poeta con grande cura ma con criteri via via diversi nel corso del tempo, caratteristica che pose agli studiosi successivi il problema della datazione delle numerose poesie non datate. L’intento di Petrarca tuttavia era ben chiaro: scrivere una sorta di autobiografia spirituale incentrata intorno all’amore non corrisposto per Laura, donna conosciuta ad Avignone quando aveva 23 anni, il 6 aprile 1327, e, come nelle migliori storie d’amore, mai più dimenticata.

Frederic J. Jones, italianista presso l’università del Galles, propose un modello che, analizzando nel corso del tempo i sentimenti di Petrarca nei confronti di Laura, e le reazioni della donna, forniva uno schema cronologico in cui incasellare in un ordine plausibile tutti i componimenti privi di data. Ecco che la matematica dell’amore stava diventando una disciplina a tutti gli effetti e compariva in un libro che sarebbe poi stato pubblicato nel 1995.
Jones ipotizzò che le emozioni di Petrarca seguissero uno schema ciclico regolare e, per dimostrare questa sua idea, utilizzò un approccio matematico che avrebbe fatto invidia a un consumato fisico sperimentale. Dopo aver condotto un’approfondita analisi stilistica e linguistica di 23 componimenti di data certa tra quelli scritti da Petrarca tra il 1330 e il 1347 (anno della morte di Laura), lo studioso assegnò alle emozioni espresse dal poeta un voto da +1 (amore estatico) a -1 (disperazione profonda); vediamo alcuni esempi:
Sonetto LXXVI
Amor con sue promesse lusingando,
mi ricondusse alla prigione antica
–> Grande amore (+0,6)
Sonetto LXXIX
Così mancando vo di giorno in giorno,
si chiusamente, ch’i’ sol me ne accorgo
et quella che guardando il cuor mi strugge.
–> Grande disperazione (-0,6)
Sonetto CLXXVI
Parme d’udirla, udendo i rami et l’ore,
et le frondi, et gli augei lagnarsi, et l’acque
mormorando fuggir per l’erba verde.
–> Malinconia (-0,45)
Un grafico in cui i voti sono espressi in relazione alla data del componimento, mostra chiaramente che l’amore di Petrarca per Laura ebbe un andamento oscillatorio con un periodo pari a circa quattro anni.
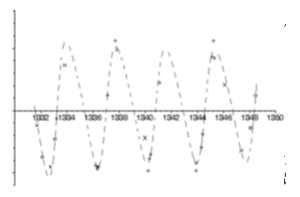
Una prima fase caratterizzata da felicità ed esaltazione, in cui i suoi sentimenti sono ricambiati da gesti di amicizia da parte della donna, si alterna a momenti di angoscia e struggimento, in cui nel poeta si acuisce sempre più la consapevolezza di non essere corrisposto; a questo punto Laura, commossa o impietosita, riprende a trattare Petrarca con affetto e a incoraggiarne i sentimenti, innescando nuovamente la fase positiva, e via di seguito. Questa analisi, integrata a informazioni sulla vita di Petrarca e sulle sue visite ad Avignone, ha consentito a Jones di ordinare cronologicamente i componimenti privi di data sulla base del “ciclo emotivo” del poeta – nonché a mostrare che è vero, o quantomeno che non è falso, che in amor vince chi fugge.
Il lavoro di Jones, qualche anno dopo, fu ripreso da un professore del Politecnico di Milano, Sergio Rinaldi, che cercò di rendere più oggettivo l’elemento introdotto dalle valutazioni dell’italianista. La matematica dell’amore, come abbiamo visto, cerca di ridurre sospiri, batticuori e romanticherie varie a una manciata di equazioni e a un pugno di grafici; trattandosi pur sempre di matematica, la sfida raccolta da Rinaldi era quella tipica del metodo scientifico: consisteva infatti nel costruire, per la dinamica amorosa del rapporto tra Laura e Petrarca, un modello indipendente che rispettasse i risultati ottenuti empiricamente da Jones.

Il modello di Rinaldi, esposto per la prima volta in un articolo nel 1998 e poi riproposto recentemente in un volume scritto a più mani, si appoggia sulla nota dinamica che esiste tra un cacciatore e la sua preda. Non conosco dettagli biografici su di lui, ma questa scelta potrebbe dirci qualcosa sul suo approccio al problema delle relazioni di coppia… Ad ogni modo, la matematica non guarda in faccia nessuno, e la matematica dell’amore non deve fare eccezioni!
Il comportamento di Laura è descritto da una singola variabile L(t), che ha valori positivi quando Laura sceglie di incoraggiare il suo devoto corteggiatore e negativi quando predomina invece il desiderio di respingerlo (forse mi ero dimenticata di scriverlo, ma Laura aveva ottimi motivi per non entusiasmarsi troppo degli ardori del poeta, essendo già maritata). Il caso di Petrarca, secondo il matematico, è un po’ più complesso, e necessita di due variabili: P(t), il suo amore per Laura, e Z(t), l’ispirazione poetica. L’amore per Laura sostiene l’ispirazione di Petrarca che, da sola, decadrebbe esponenzialmente; integrando le equazioni si scopre che, subito dopo il primo incontro con la donna, l’ispirazione cresce molto più lentamente della passione ma poi, per l’intero periodo esaminato, assume sempre valori positivi. Questo dato ben si accompagna al fatto che Petrarca scrisse il primo componimento dedicato a Laura soltanto più di tre anni dopo averla conosciuta; dopo di che, tuttavia, la sua produzione continuò con regolarità, senza nessuna interruzione significativa. Mentre è ragionevole supporre che il comportamento di Petrarca possa essere descritto da una funzione lineare, nel caso di Laura le cose stanno diversamente: come abbiamo già accennato descrivendo il modello di Jones, sebbene fosse del tutto normale, per una donna dell’alta società dell’epoca, incentivare i propri corteggiatori con sguardi e sorrisi, esiste in Laura un elemento antagonista che tende invece a scoraggiare gli slanci amorosi del poeta quando essi si fanno troppo espliciti oppure, addirittura, a respingerlo pubblicamente, facendolo così precipitare nella più nera disperazione.
Complessivamente, i risultati di Rinaldi sono in buon accordo con quelli ottenuti da Jones; i due modelli sono indipendenti, ma anche quello di Rinaldi prevede una buona dose di soggettività nella valutazione dei parametri delle equazioni. Su questo sito, se proprio vi siete appassionati alla questione, è possibile visualizzare i risultati delle equazioni rappresentati graficamente e anche variare i valori dei parametri assegnati dall’autore.

E’ ovvio che modelli come quelli descritti sono, per talmente tanti motivi che proverò a elencarne qualcuno ma mi sento ridicola anche solo a iniziare, una cruda semplificazione della realtà: l’amore è un insieme di sentimenti diversi (stima, amicizia, affetto, attrazione…) e, pertanto, certo non catturabile da una o due o anche tre variabili; senza contare che tutte le tensioni e le emozioni vissute da una persona, che oltre alle proprie estreme complessità individuali è inevitabilmente inserita in un contesto sociale, non possono essere racchiuse in una singola equazione. E poi che dire del fatto che l’amore è cieco, gli opposti si attraggono, l’unica legge dell’amore è che non ha leggi e via discorrendo?
Pur tuttavia, la scienza procede aggiungendo a ogni gradino un granello di difficoltà e un pizzico di complessità; non è dunque detto che, fra non molto tempo, sistemi di equazioni differenziali dall’aspetto inquietantemente asettico saranno abbastanza attendibili da farci venir voglia di affidarci a loro come guida nelle scelte relazionali. D’altronde, non è che a oggi ci siano tante altre soluzioni particolarmente convincenti alle questioni di cuore…
Per il momento, se non altro, io mi accontento di aver imparato una ulteriore applicazione del calcolo differenziale di cui non sospettavo minimamente l’esistenza; così come l’amore, in fin dei conti anche la matematica si muove in modi del tutto misteriosi.
*La storia della querelle tra Newton e Leibniz è nota e dà un’idea molto chiara del fatto che i matematici, oltre a trascorrere il tempo a riflettere e scrivere equazioni, sanno essere anche piuttosto… aggressivi, quando è in gioco la loro reputazione. Meno nota, almeno in Italia, è una figura che ha fatto da trait d’union tra le opere di questi due immensi pensatori, traducendole, per l’appunto, in francese (ecco il perché di tutti questi francesismi): sto parlando della marchesa Émilie du Châtelet, di cui ho raccontato la vita appassionante di scienziata, matematica dell’amore (anche se in un senso un po’ diverso) e traduttrice in questo articolo.




